В начало поста вынесен эпиграф к книге "Путешествие из Петербурга в Москву" Александра Николаевича Радищева (1749-1802), что в переводе означает "Чудовище тучное, гнусное, огромное, стозевное и лающее". Это, пожалуй, самый точный* "портрет" системы символьных вычислений Maxima после логичности, простоты и превосходной документации Maple.Открыть в полный размер' href="http://1.bp.blogspot.com/_hM8AMxgJLzw/TRg3MDWaCbI/AAAAAAAABhY/LPuYIG921U8/s1600/wxMaxima_2.png" target=_blank style=color:white;>Открыть в полный размер' href="http://1.bp.blogspot.com/_hM8AMxgJLzw/TRg3MDWaCbI/AAAAAAAABhY/LPuYIG921U8/s1600/wxMaxima_2.png">
В инженерной практике очень часто бывает необходимо по-быстрому взять интеграл, продифференцировать длинное и занудное выражение, сложить пару километровых матриц или ещё чего по мелочи. Делать это от руки, хотя и можно, но лениво - вот тут нам и пригодится система компьютерной алгебры Maxima, которая есть в любом уважающем себя дистрибутиве.
Установка Maxima
Скачивать Maxima с варёзных сайтов, в отличие от Maple, не надо (а если всё-таки надо, скачать Maxima бесплатно можно наофициальном сайте). В Debian просто устанавливаем: aptitude install wxmaxima maxima
Стоит подчеркнуть, что без wxmaxima, которая предоставляет возможность копирования результатов в LaTeX, автозакрытия двоеточием и форматированным выводом, сама Maxima почти бесполезна и крайне раздражает своим невменяемым интерфейсом - настолько, что чаще сделать всё от руки проще и быстрее.
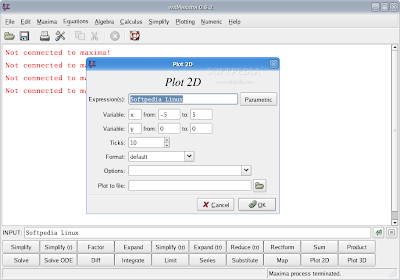
Графическая оболочка сильно выправляет ситуацию с идиотскими косяками текстового режима и делает Maxima в целом съедобной. В конце команды не забываем написать точку с запятой, если работаем с консольным интерфейсом. В графической среде это сделают за нас.
Выход из Maxima
Это достойно интерфейса одного текстового редактора, который пищит и всё портит. Чтобы выйти из Maxima, нужно дать команду: quit();
Как признаётся даже официальная документация, "This is a bit confusing for new users, but you must type that full command". Почему бы не наступить на горло собственной песне и сделать хотя бы вот это просто и пряморуко, автор понять не в силах. Опять-таки, графический интерфейс всё делает за нас.
Простые вычисления
Вот есть у нас выражение типа x^2 , и мы хотим его вычислять, меняя x. Это достигается следующей хитроумной конструкцией:
(%i2) at (x^2, [x=7]);
(%o2) 49
(%i3)
Или ещё. Если мы хотим упрощать что-то вроде a - b + 2*a то Maxima это надо разжевать, положить в ротик, залить кипяточком и хорошенько пнуть:
(%i19) K(s):= s^2+2;
(%i22) expand(K(s)-s^2);
(%o22) 2
То есть функция eval тут не проходит, обязательно expand. И функцию объявляем с явным прописыванием переменной вот так: K(s):= s^2+2;
Ну и наконец, как выглядит мнимая единица в Maxima? Вот как:
(%i12) (0.1*%i)^2;
(%o12) -0.01
То есть i это в Maxima вот так: %i
Матрицы
Так как по роду приходится иметь дело с линейной алгеброй и (отчасти) символьными вычислениями, приходится иметь дело с оценкой свойств матриц. В силу того, что я ленивый и несколько забывчивый, мне приходится использовать Maxima с её откровенно наркоманским интерфейсом считать матрицы, особенно если они параметрические.
Определение матрицы
(%i16) A: matrix([1,e],[3,4]);
[ 1 e ]
(%o16)
[ ]
[ 3 4 ]
То есть строки набиваются через [], разделение строк и каждого элемента - запятая.
Простейшие операции с матрицами
Например, нужно нам матрицу умножить саму на себя, но это будет параметрическая матрица:
(%i1) A: matrix([a,b],[c,d]);Теперь умножим матрицу саму на себя. Казалось бы, это очевидно: K*K даст желаемый результат:
[ a b ]
(%o1) [ ]
[ c d ]
(%i15) K*K;
[ 2 2 ]
[ a b ]
(%o15)
[ ]
[ 2 2 ]
[ c d ]
Однако это вызывает удивлённую реакцию в формате "что за ...?". Дело в том, что очевидное у пользователей и у программистов Maxima разное, и операция K*K даст нам поэлементное умножениематрицы. А чтобы получить обычное матричное умножение (строка на столбец), используем операцию K.K и получаем:
(%i16) K.K;
[ 2 ]
[ b c + a b d + a b ]
(%o16) [ ]
[ ]
[ c d + a c d + b c ]
искомое умножение матриц. Подсыпаем ещё подосиновиков в турбокальян, и, попыхивая чёрным дымом, медленно двигаемся дальше.
Упрощение\выполнение символических вычислений
Пусть у нас есть перемножение нескольких матриц, ячейки которых содержат параметры. Мы слишком ленивы (и это правильно), чтобы делать это вручную, поэтому попробуем запрячь Maxima на выполнение этого. Например, умножили несколько матриц, и хочется развернуть алгебраическое выражение в каждой ячейке:
(%i21) A*A1.A;
[ c (c c1 + b b1) b (b c1 + b1 c) ]
(%o21) [ ]
[ b (b c1 + b1 c) c (c c1 + b b1) ]
Тут можно бы предположить, что пройдёт вариант с функцией evесли использовать её как detout:
(%i22) ev A*A1.A;
Incorrect syntax: a is not an infix operatorevSpaceA*^
Тут нас облаяли, но и синтаксис:
(%i22) ev(A*A1.A);
[ c (c c1 + b b1) b (b c1 + b1 c) ]
(%o22) [ ]
[ b (b c1 + b1 c) c (c c1 + b b1) ]
желаемого не даёт. А жаль. Впрочем, Капитан Документация спешит на помощь: нужна функция expand:
(%i23) expand(A*A1.A);
[ 2 2 ]
[ c c1 + b b1 c b c1 + b b1 c ]
(%o23) [ ]
[ 2 2 ]
[ b c1 + b b1 c c c1 + b b1 c ]
Это сэкономило нам пять минут ручной работы, но прибавило десять минут поиска в документации. Неплохо, бывало и хуже.
Вычисление детерминанта матрицы в Maxima
Это делается сравнительно длинной командой determinant:
(%i17) determinant(A);
(%o17) 4 - 3 e
Автодополнением в консоли даже не думайте пользоваться: оно всё заменит на ЗАГЛАВНЫЕ БУКВЫ и вычислять откажется, что в общем ставит вопрос вменяемости разработчиков ещё острее.
Производные
Для вычисления производных испольуем функцию diff в формате
diff ( f(x), x, k)
где:
f(x) == дифференцируемая функция
x == переменная, по которой следует дифференцировать
k == порядок производной (k=1 - первая производная, k=2 - вторая производная)
Учебник математического анализа, возможно, ещё не стёрся из памяти читателя окончательно, так что посмотрим на примеры. Берём первую первую производную от функции 1/(s+1)^2 по переменной s и получаем:
(%i14) diff(1/(s+1)^2,s);
2
(%o14) - --------
3
(s + 1)
Вторая производная от той же функции:
(%i15) diff(1/(s+1)^2,s,2);
6
(%o15) --------
4
(s + 1)
Всё работает правильно.
Преобразование Лапласа
Если вы занимаетесь или изучаете теорию автоматического управления (Control Theory), вам очень даже пригодится прямое и обратное преобразование Лапласа (Laplace Transform)
Для расчёта
(%i8) ilt(1/(1+s^2)^2,s,t);
sin(t) t cos(t)
(%o8) ------ - --------
2 2
(%i6) laplace(1,t,s);
1
(%o6) -
s
Автор недоумевает по поводу отсутствия такой тривиальной вещи в Максиме, как Z-transform. Вроде бы Максиме не полгода, и цифровые контроллеры сейчас вроде как распространены достаточно, чтобы об этом подумать. Но не здесь.
Заключение и дискуссии
В целом: MAXIMA можно пользоваться ТОЛЬКО с графическим интерфейсом, который нужно устанавливать сразу же. Пакет в Debian называется wxmaxima и особенно при первом знакомстве будет очень кстати. Максима страдает обычными опенсорсными болячками: дурная документация и не всегда логичный командный интерфейс. Если же заткнуть нос и уши, поставив wxmaxima, Максимой пользоваться можно с некоторым даже комфортом: вы даже сможете копировать выхлоп Максимы в формате ЛаТеХ.
Ссылки
Имеет место быть, хотя и довольно топорная, но всё-таки официальная документация. В разогретый кальян хорошо бы покрошить ссылки о базовых способах вычислений в Maxima.
У издательства Alt Linux, как выясняется, есть очень неплохая книга Е.А. Чичкарева "Компьютерная математика с Maxima".
Стараниями уважаемых комментаторов нашёлся:
- хороший "10-ти минутный туториал" по Максиме (ин инглиш),
- примеры из книжки Maxima by Example,
- ещё примеры (теперь уже на русском)
- подборка из журнала LinuxFormat про Maxima.
Ежели отряды Анонимусов, достигших просветления поболе автора, накидают ещё ссылок, автор их (ссылок, не Анонимусов) вставит в пост с удовлетворением и искреннею радостию.