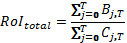Термин "окупаемость инвестиций" (return on investment - ROI) часто используется для описания выгоды от инвестиций в программное обеспечение и системы и от других бизнес-инвестиций. Для улучшения распределения инвестиций необходимо получить ROI-ответы на различные бизнес-вопросы: Как окупились предыдущие инвестиции? Нужно ли продолжать инвестировать данный проект? Какова будет общая окупаемость инвестиций за время жизни программного обеспечения или системы? В данной статье рассматриваются различные методики вычисления окупаемости инвестиций для получения ответов на эти вопросы.

Введение

Мы часто говорим об окупаемости инвестиций в программное обеспечение, систему или ИТ-проект, чтобы обосновать решение о работе над ними. Иногда это звучит абстрактно, поскольку мы говорим, что окупаемость инвестиций в определенное ПО будет выше, не называя численных показателей этой эффективности. Поэтому нужны точные определения окупаемости инвестиций. Их существует несколько, и каждое из них можно использовать для принятия различных решений. В данной статье описываются идеи, заложенные в расчеты. Подробные формулы приведены в Приложении 3.

Вычисление будущего

Кто-то однажды сказал: "Невозможно предсказать будущее, но это наша работа". Тому, кто ответственен за обоснование величины будущих инвестиций, приходится работать с неполной информацией. Например, невозможно знать наверняка, каков будет доход от нового продукта. Тем не менее эта цифра необходима нам для расчета ожидаемой окупаемости вывода данного продукта на рынок. К счастью существует путь, по которому можно идти.

В следующем разделе представлено несколько подходов к оценке окупаемости инвестиций с соответствующими расчетами. При работе с приведенными ниже уравнениями вместо фиксированных значений можно использовать случайные переменные (см. Приложения 1 и 2). В современном бизнес-анализе часто используются случайные переменные с треугольными распределениями, описанные в Приложении 1.

Примечания:

• Если вы уже знакомы с концепциями случайных переменных, продолжайте чтение статьи. Если нет, полезно сначала прочитать приложения.
• Полезно также прочитать введение в определение стоимости продолжения разработки, приведенное в моей предыдущей статье "Расчет и повышение окупаемости инвестиций в программное обеспечение и системы", опубликованной в ежемесячном журнале Communications of the Association for Computing Machinery (цифровая версия) в сентябре 2011 года. В данной статье приведена точная формула, реализующая идею вышеуказанной предыдущей статьи из журнала.

To-dateROI и To-goROI

Для начала скажем, что все виды ROI основаны на одной базовой концепции: окупаемость инвестиций, вообще говоря, представляет собой отношение изменения стоимости к стоимости инвестиций. В данной формуле V₀ - это некая начальная стоимость, V₁ - более поздняя стоимость, а I - сумма денег, потраченных за это время:

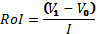
Эта формула применяется по-разному в зависимости от вида активов.

Простейший пример ROI - обоснование определенных капитальных вложений, например акций, покупаемых по одной цене и продаваемых по другой. В расчете известны две величины, которые устанавливаются законами рынка: стоимость покупки (purchase price - pp) и стоимость продажи (sales price - sp). Здесь ROI - это отношение изменения стоимости к стоимости покупки акции. В данном случае:

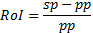
Но даже здесь возможны варианты. Предположим, что профессиональный инвестор имеет два ключевых вопроса:

To-date

Хороша ли ранее сделанная инвестиция (какой будет ROI, если продать сегодня)?
 

To-go

Нужно ли инвестировать в данный актив сейчас (какой будет ROI, если купить несколько этих активов сегодня)?
 

Первый вопрос является ретроспективным, так как показывает, насколько хорошо инвестор принимает решения. Ответ может изменить стратегию инвестирования. Второй вопрос является частью реализации стратегии инвестирования. Естественно, ответ на эти вопросы требует различных расчетов ROI:

To-date

Здесь V₁ - это сегодняшняя стоимость (суммарный доход от продажи всех акций по текущей цене) плюс вся прибыль, полученная инвестором до данной даты (например, дивиденды), а V₀ и I - это сумма всех инвестиций в данные активы.
 

To-go

Здесь V₁ - это оценочный доход от продажи активов в будущем, V₀ - это начальная стоимость активов, а I - сумма ожидаемых затрат на инвестиции, начальной стоимости и будущих выплат.
 

Важно!
Эти ситуации практически полностью независимы. Предыдущие затраты (уже сделанные), используемые в to-date, отсутствуют в to-go.

Возвращаясь к первому уравнению, в анализе инвестиций (IA) To-date ROI - это случайная переменная, где

• V1 = NPV _{сегодня} + сумма фактической прибыли на данную дату
• V0 = NPV_{в начале программы}
• I = сумма затрат на данную дату

Отметим, что I основывается на фактических расходах. В большинстве случаев имеет смысл установить NPV _{в начале программы} в ноль.

Для IA-программ "конец жизни" наступает, когда все затраты и прибыль заканчиваются. В этот момент стоимость равна нулю. В целом IA-инвестиция обесценивается после осуществления.

В To-go ROI все прошлые затраты и прибыль игнорируются. Имеют значение только дисконтированные будущие расходы и прибыль. Применим базовое уравнение для получения следующей формулы:

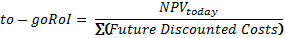
Расчеты NPV и будущих затрат включают в себя будущие значения, используемые как случайные переменные в IA, поэтому в данной формуле для анализа инвестиций применяется метод Монте-Карло (см. Приложение 2).

Совокупная ROI

Учитывая, что IA содержит реальные и прогнозируемые затраты и прибыль, можно выполнить другие полезные расчеты ROI. Например, вы хотите инвестировать в программу в случае обоснованной ожидаемой доходности в течение всей жизни инвестиции. В этом случае можно рассчитать прогнозируемое значение To-date ROI в конце программы. Поскольку стоимость в конце программы отсутствует, установив NPV _{в начале программы} в ноль, находим:

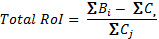
При окончании программы подставляются фактические значения. До этого можно спрогнозировать total ROI , используя смесь дисконтированных будущих значений и фактических значений. В данном случае total ROI - это случайная переменная, определяемая при помощи IA-метода Монте Карло.

Ссылочные даты

Прогнозы ROI обычно рассчитываются на сегодняшний день. Однако, поскольку IA содержит все затраты и прибыли инвестиции (прошлые значения как фактические, а будущие как случайные переменные), для расчетов можно установить любую ссылочную дату. Т.е. можно спрогнозировать распределение NPV , а также To-go ROI и To-date ROI на любую дату в будущем. Например, это может быть дата осуществления. Можно предсказать значения на момент времени, когда продукт начнет приносить прибыль. Может представлять интерес сравнение двух инвестиций с различной датой осуществления.

Примечание.
Total ROI представляет собой прогнозируемую To-date ROI с окончанием программы в качестве даты осуществления.

Заключение

Окупаемость инвестиций (ROI), вообще говоря, представляет собой отношение прибыли к затратам. Каждый, кто ограничен в средствах, хочет использовать инвестиции с максимальной выгодой. Даже для простых инвестиций существует несколько видов ROI, каждый из которых отвечает на различные вопросы. В данной статье рассмотрены три самых полезных варианта:

• To-date: какую прибыль принесет сделанная инвестиция?
• To-go: какая прибыль ожидается от будущих инвестиций?
• Total: какую окупаемость можно ожидать от всех инвестиций по окончании программы?

Подробные формулы приведены в Приложении 3.

Приложение 1. Случайные переменные

Предположим, что вы не уверены в значении, которое хотите использовать. Например, объем будущих продаж непоставленного товара может быть важен, но никто не может быть уверен в его фактической стоимости. В современной бизнес-аналитике принято указывать такие неопределенные величины как случайные переменные . Ниже приводится краткое описание их использования. (Значительно больше информации приводится в книге Дугласа Хаббарда (Douglas Hubbard) "Как измерить что угодно: определение стоимости нематериальных активов в бизнесе" (2-я редакция), Wiley, 2010 год). Поскольку мы не уверены на 100% в будущем значении, лучше всего указать, что значением v может быть любое значение в определенном диапазоне. Например:

a ≤ v ≤ b

Этим мы говорим, что значение v меньше a или больше b с вероятностью ноль (в некоторых случаях мы можем допустить, что a равно -∞ или b равно ∞). Мы также говорим, что значение v находится между a и b с вероятностью 1. Можем пойти дальше и предположить, что некоторые значения v более вероятны, чем другие. В этом случае можно указать вероятность каждого возможного значения v . Следовательно, у нас имеется кривая зависимости каждого возможного значения v и вероятности этого значения v . Итак, случайная переменная является числом, описываемым кривой, которая для каждого значения в диапазоне определяет вероятность того, что переменная примет это значение. Кривая называется распределением вероятности случайной переменной.

Важным свойством распределений является то, что поскольку случайная переменная должна принимать некоторое значение, сумма вероятностей значений должна равняться единице.

Например, когда мы берем лучший случай (H), худший случай (L) и наиболее вероятное значение (E) объема будущих продаж, мы можем указать случайную переменную с распределением, представленным на рисунке 1.

Рисунок 1. Треугольное распределение для случайной переменной

Высота кривой в каждой точке представляет вероятность того, что переменная примет это значение. Поэтому мы выбрали распределение с нулевой вероятностью ниже L или выше H с пиковым значением в точке E. Высоты выбирались так, чтобы площадь треугольника (сумма всех вероятностей) была равна 1. В этом случае вероятность того, что v примет значение около L или H низка, а вероятность значения около E относительно высока.

Естественно, распределение может принимать форму любой кривой с учетом того, что площадь под этой кривой должна равняться единице.

Итак, случайная переменная - это величина, которая может принимать любое значение. Однако некоторые значения более вероятны, чем другие. Т.е. случайная переменная определяется функцией, которая каждому значению присваивает вероятность. Эта функция называется распределением вероятности случайной переменной.

Приложение 2. Вычисления со случайными переменными: метод Монте Карло

Предположим, мы хотим сложить две случайные переменные v ₁ и v ₂ . Как это сделать? Во-первых, отметим, что сумма тоже должна быть случайной переменной. Следовательно, нам необходимо распределение вероятности суммы. Для этого распределения нет формулы, но существует эффективный, широко используемый численный подход, известный как моделирование методом Монте Карло .

Идея состоит в использовании генератора случайных чисел для генерирования значения v ₁ , значения v ₂ , а затем их суммирования. Значения выбираются согласно распределению вероятности каждой переменной. Более вероятные значения генерируются чаще. Теперь сохраним эту сумму и повторим процедуру много раз, скажем 100000, и сохраним каждую сумму. Для каждой суммы можно вычислить вероятность, определив частоту ее появления в массиве сохраненных сумм (некоторые суммы появляются чаще остальных) и разделив на число отсчетов данных (необходимо округлить суммы для получения дискретных чисел). Мы получим приблизительное распределение сумм.

Рассмотрим пример, где v ₁ имеет треугольное распределение с L = 3, E = 4, H = 7 (см. рисунок 2), а v ₂ имеет треугольное распределение с L = 1, E = 6, H = 7 (см. рисунок 3).

Рисунок 2. График треугольного распределения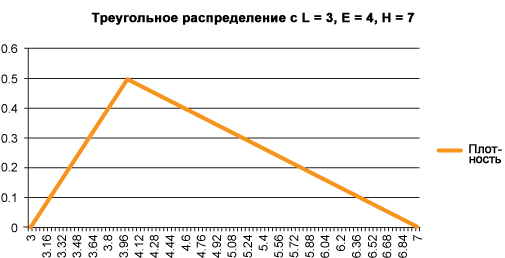

Рисунок 3. График треугольного распределения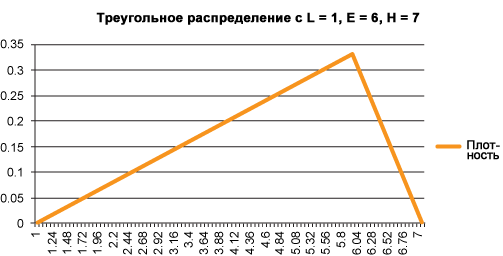

На рисунке 4 представлено распределение суммы двух случайных переменных, показанных на рисунках 2 и 3, найденное методом Монте Карло. Было использовано 100000 отсчетов, а расчет проводился в IBM Rational Focal Point.

Рисунок 4. Смоделированное распределение суммы (из 100000 отсчетов)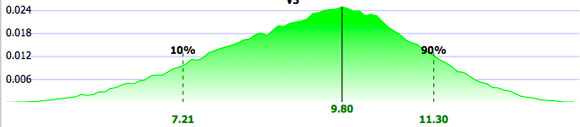

Во-первых, отметим, что сумма уже не является треугольным распределением, а больше похожа на нормальное распределение, имеющее вид колоколообразной кривой. Пик (мода) распределения находится 9.80. Это и ожидалось исходя из теории вероятностей (в частности, центральной предельной теоремы). Такое распределение суммы выглядит разумно. Например, можно ожидать, что наиболее вероятное значение суммы будет равно 10, т.е. сумме двух наиболее вероятных значений, но в нашем примере оно равно 9.8. Расхождение является случайным и исчезает с увеличением количества отсчетов. Также отметим, что вероятность падает до нуля ниже 4, суммы минимумов (на рисунке 4 не выделено, но очевидно), и выше 14, суммы максимумов.

Наконец, фиксированные и случайные переменные легко комбинируются. Фиксированную переменную можно рассматривать как случайную, вероятность единственного значения которой равна 1, а вероятность всех остальных значений равна нулю.

Приложение 3. Формулы ROI

Предположим, что в нашей программе имеется T временных интервалов, N_B идентифицированных прибылей и N_C идентифицированных затрат. Отметим, что каждая статья расходов и прибыли является временной последовательностью значений. Тогда:

• Для 0 ≤ t ≤ T и 1 ≤ n ≤ N_B 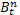это значение n -ой прибыли на интервале t .
• Для 0 ≤ t ≤ T и 1 ≤ m ≤ N_c 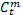это значение m -ых затрат на интервале t .

Здесь важно отметить, что все временные последовательности пересматриваются в течение жизненного цикла, т.е. они зависят от времени. Временные последовательности собираются в виде последовательностей зафиксированных данных. Поэтому по мере поступления информации случайные переменные должны обновляться в течение жизненного цикла. Со временем оценки превращаются в реальные значения, а будущие значения обновляются. На практике каждое значение временных последовательностей прибыли и затрат тоже зависит от времени. Более подробно эта тема рассмотрена в разделах To-date и To-go ROI и Total ROI.

B^k(s) и C^l(s) - это зафиксированные потоки прибыли и затрат. Чтобы не загромождать изложение, мы будем опускать фиксированную переменную, когда в ней нет необходимости. Нам потребуется еще несколько условных обозначений:

• r - это расчетный период для вычислений, текущий период или какой-либо период в будущем.
• Для 1 ≤ n ≤ NB rbn = ставка дисконтирования прибыли Bn .
• Для 1 ≤ m ≤ NB rcm = ставка дисконтирования затрат Cm .
• Для данного периода t и расчетного периода r сумма всех дисконтированных прибылей на t по отношению к r будет равна:
  

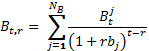
• Аналогично, для данного периода t и расчетного периода r сумма всех дисконтированных затрат на t по отношению к r будет равна:

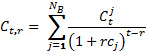
Отметим, что значения временных последовательностей могут быть случайными переменными, фиксированными переменными или и теми, и другими. В любом случае по мере необходимости их можно суммировать по методу Монте Карло.

В следующем выражении определяется чистая дисконтированная стоимость (net present value - NPV) за период r:

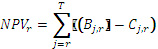
Затем:

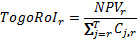
Отметим, что для двух любых периодов s и t :

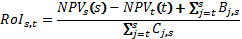
В этом вычислении TodateROI_s является специальным случаем ROI_s,0 . В этом случае B_j,s и C_j,s - это, как правило, фактические значения.

Наконец, Todate ROI - это ROI_T,0 .

По определению конца жизни NPV_T= 0 , поскольку не остается затрат или прибылей. Также в большинстве случаев NPV ₀ близка к 0, поскольку все затраты находятся в будущем. Таким образом, установив NPV₀ в 0, получим: